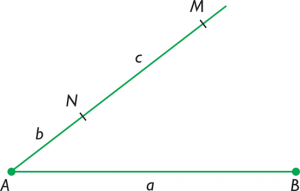
La bisectriu és la recta que divideix en dues parts iguals a un angle; es tracta del lloc geomètric dels punts del pla que equidisten, és a dir, es troben a la mateixa distància de les semirectes d'un angle. Val a destacar que es diu lloc geomètric al conjunt de punts que satisfan unes determinades propietats geomètriques i semirecta a cadascuna de les dues parts en què queda dividida una recta per qualsevol dels seus punts, és a dir, és la part de la recta conformada per tots els punts que s'ubiquen cap a un costat del punt fix de la recta; aquesta té un primer punt o origen i com que la resta de les rectes s'estén cap a l'infinit.
Mentrestant, el punt de la bisectriu serà equidistant a les dues rectes de l'angle. Com a conseqüència de la reciprocitat, quan dues rectes es creuen determinaran quatre angles i cadascun definirà una bisectriu.
Per la seva banda, als triangles, les tres bisectrius dels angles interns d'un triangle es tallaran en un únic punt, que es mostrarà equidistant respecte dels costats; a aquest punt se'l coneix com incentre del triangle i serà el centre de la circumferència inscrita al triangle en qüestió.
El teorema de la bisectriu de l'angle intern d'un triangle és un teorema que correspon a la geometria elemental i sosté que en un triangle, la raó entre dos costats serà igual a la raó de les parts en què quedarà dividit el tercer costat per la bisectriu de l'angle intern oposat .
