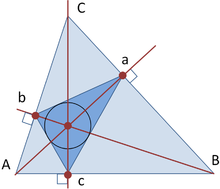
La paraula ortocentre és un terme que s'usa excloentment dins de l'àmbit de la Geometria i refereix a aquell punt d'intersecció on conflueixen les tres altituds d'un triangle. És a dir, a l'ortocentre es tallen les tres altures d'un triangle. Se'l simbolitza a partir de la lletra H majúscula.
El triangle, per la seva banda, és un polígon definit per tres rectes, les quals es tallen dos a dos en tres punts que no s'hagin alineats; els punts en què s'uneixen les rectes s'anomenen vèrtexs i les porcions de recta que queden determinades són els costats del triangle.
Cal destacar que l'ortocentre no resulta gens una qüestió insignificant atès que per exemple tres rectes qualsevol que es prenen a parells es tallaran en tres punts diferents, en canvi, en el cas dels triangles, les altures es tallen en un mateix punt i això és molt simple i senzill de demostrar a partir de justament l'ortocentre.
Quan el triangle és acutangle, és a dir, els seus tres angles interiors són menors a 90°, l'ortocentre serà el incentre del triangle òrtic, que és aquell que presenta com a vèrtexs als peus de les tres altures, val a dir, les projeccions dels vèrtexs sobre els seus costats. Mentrestant, l'incentre, simbolitzat a partir de la lletra I, serà aquell punt en què s'intersequen les tres bisectrius dels angles interiors del triangle i crea la circumferència inscrita al centre del triangle en qüestió.
D'altra banda, si el triangle és rectangle, aquell que disposa d'un angle recte de 90°, l'ortocentre coincidirà amb el vèrtex de l'angle recte esmentat.
I si es tracta d'un triangle obtusangle, quan un dels seus angles interiors és obtús, és a dir, major a 90° i els altres dos mesuren menys de 90°, l'ortocentre s'ubicarà per fora del triangle.
