El concepte d'identitats trigonomètriques és un concepte que s'utilitza a l'àmbit de les matemàtiques per fer referència a les funcions trigonomètriques variables que es poden trobar en una figura geomètrica. La trigonometria és la branca de les matemàtiques que s'especialitza en l'anàlisi i l'estudi dels triangles, especialment en les formes, els significats i els valors dels diferents angles que poden existir. Les identitats trigonomètriques seran, doncs, els resultants d'aquests valors que són variables i molt diversos entre l'un i l'altre.
Tal com passa amb molts elements de les matemàtiques, els conceptes existeixen des d'èpoques antigues en què els filòsofs grecs ja havien establert les nocions de funcions i valors dels angles de les figures geomètriques. Aquests conceptes serien millorats recentment a la Modernitat, al segle XVII quan es van notar de manera algebraica per poder realitzar tot tipus de càlculs entre els diferents angles.
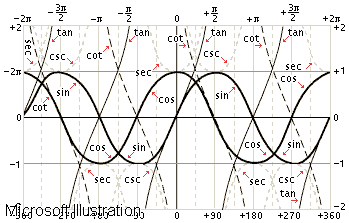
Les identitats trigonomètriques es poden definir en termes generals com totes les variables possibles d'angles que poden existir en una figura geomètrica. Aquestes identitats es representen sempre a partir de les lletres gregues com ara alfa, beta, omega, etc. També es fan servir elements com els graus centígrads per establir les variables de cada identitat. Les més conegudes són les que s'estableixen entre sinus i cosinus, sinus i tangents, etc. Les identitats trigonomètriques són formes simplificades que permeten fer i conèixer les diferents funcions de la trigonometria. Totes aquestes qüestions de les matemàtiques, més específicament de la trigonometria, serveixen per organitzar els diferents càlculs que cal fer a partir de les funcions específiques de cada tipus de dades. Les identitats trigonomètriques són molt variables i permeten tenir diferents possibilitats per representar cada funció trigonomètrica (és a dir, els valors) de maneres variades i específiques segons cada cas.
